Ch1.1 The Continuum of Numbers

2023-11-24

访问

The only evident reason for the widespread use of the decimal system is the ease of counting by tens on our fingers(digits).

e. Inequalities

basic rules

Suppose that and are positive and is a positive integer. In the factorization

$a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+\cdots+b^{n-1})$

the second factor is positive. Thus has the same sign as . If , then and if , then , it follows that the converse is also true; that is, if , then .

Triangle Inequality

definition

$|a+b|\le |a| + |b|$

for any real .

The name “triangle inequality” is more appropriate for the equivalent statement

$|\alpha - \beta | \le |\alpha - \gamma| + |\gamma - \beta|$

for which we have set . The geometrical interpretation of this statement is that the direct distance from to is less than or equal to the sum of the distances via a third point ; (this also corresponds to the fact that in any triangle the sum of the two sides exceeds the third side).

proof

We distinguish the cases and .

In the first case: ; this follows trivially by the addition of the inequalities and .

In the second case: , which again follows by addition from .

generalize

We immediately derive analogous inequality for three quantities:

$|a+b+c| \le |a| + |b| + |c|;$

for, by applying the triangle inequality twice,

$|a+b+c| = |(a+b)+c| \le |a+b| + |c| \le |a| + |b| + |c|.$

In the same way, the more general inequality

$|a_1+a_2+\cdots+a_n| \le |a_1| + |a_2| + \cdots + |a_n|$

is derived.

Occasionally we need estimates for from below. We observe that

$|a| = |(a+b) + (-b)| \le |a+b| + |-b| = \le |a+b| + |b|$

and hence that the inequality

$|a+b|\le |a| - |b|$

holds.

The Cauchy-Schwarz Inequality

definition

$(a_1b_1+a_2b_2+\cdots+a_nb_n)^2 \le (a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2).$

Putting

$A = a_1^2+a_2^2+\cdots+a_n^2,\\\\ B = a_1b_1+a_2b_2+\cdots+a_nb_n,\\\\ C = b_1^2+b_2^2+\cdots+b_n^2,$

the inequality becomes .

proof

To prove it we observe that for any real

$0\le (a_1+b_1)^2+(a_2+b_2)^2+\cdots+(a_n+b_n)^2$

since the right-hand side is a sum of squares. Expanding each square and arranging according to powers of , we find that

$0\le A + 2Bt + Ct^2$

for all , where have the same meaning as before. Here . We may assume that , since certainly when . Substituting then for the special value ;

corresponding to the minimum of the quadratic expression

$A + 2Bt + Ct^2 = C\left(t + \frac{B}{C}\right)^2 + \left(A - \frac{B^2}{C}\right),$

we find

$0\le A - \frac{-2B^2}{C} + \frac{B^2}{C} = \frac{AC - B^2}{C}$

and hence .

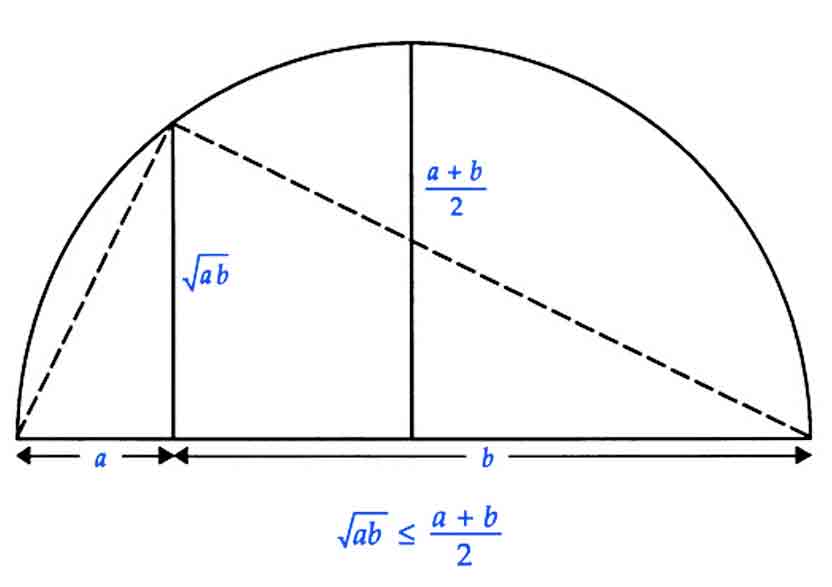
Figure 1 Geometric and arithmetic means of x and y.

In the special case we can choose

$a_1 = \sqrt{x},~~~~a_2=\sqrt{y},~~~~b_1=\sqrt{y},~~~~b_2=\sqrt{x},$

where and are positive numbers. The inequality then takes the form or

$\sqrt{xy} \le \frac{x+y}{2}.$

This inequality states that the of two positive numbers never exceeds their . The geometric mean of two numbers can be interpreted as the length of the altitude of a right triangle dividing the hypotenuse into segments of length and respectively. The inequality then states that in a right triangle the altitude does not exceed half the hypotenuse(see Fig. 1).